This website uses cookies so that we can provide you with the best user experience possible. Cookie information is stored in your browser and performs functions such as recognising you when you return to our website and helping our team to understand which sections of the website you find most interesting and useful.
- Solutions
- Products
-
- Alchemer Survey
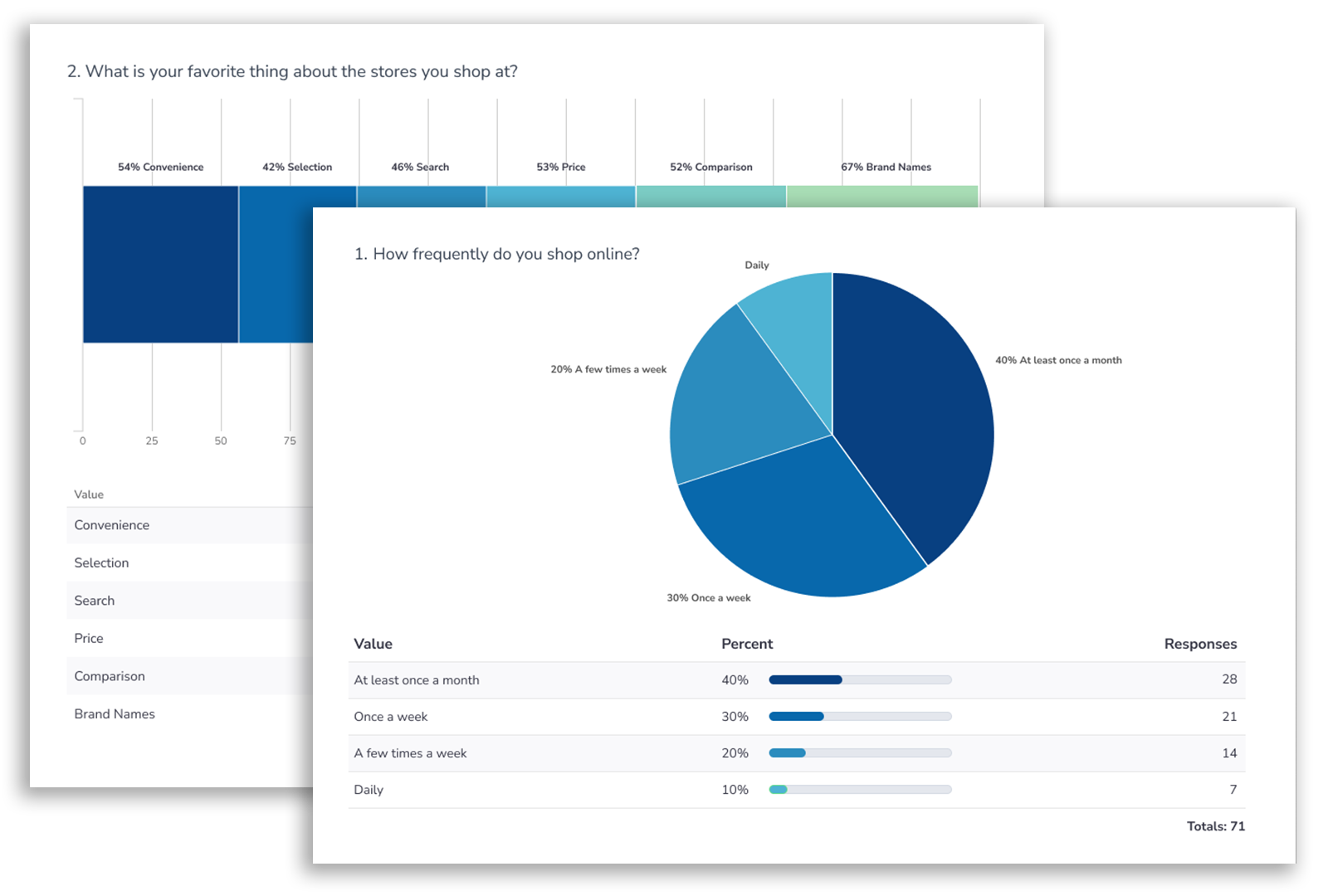
- Alchemer Survey is the industry leader in flexibility, ease of use, and fastest implementation.Learn More
- Alchemer Workflow
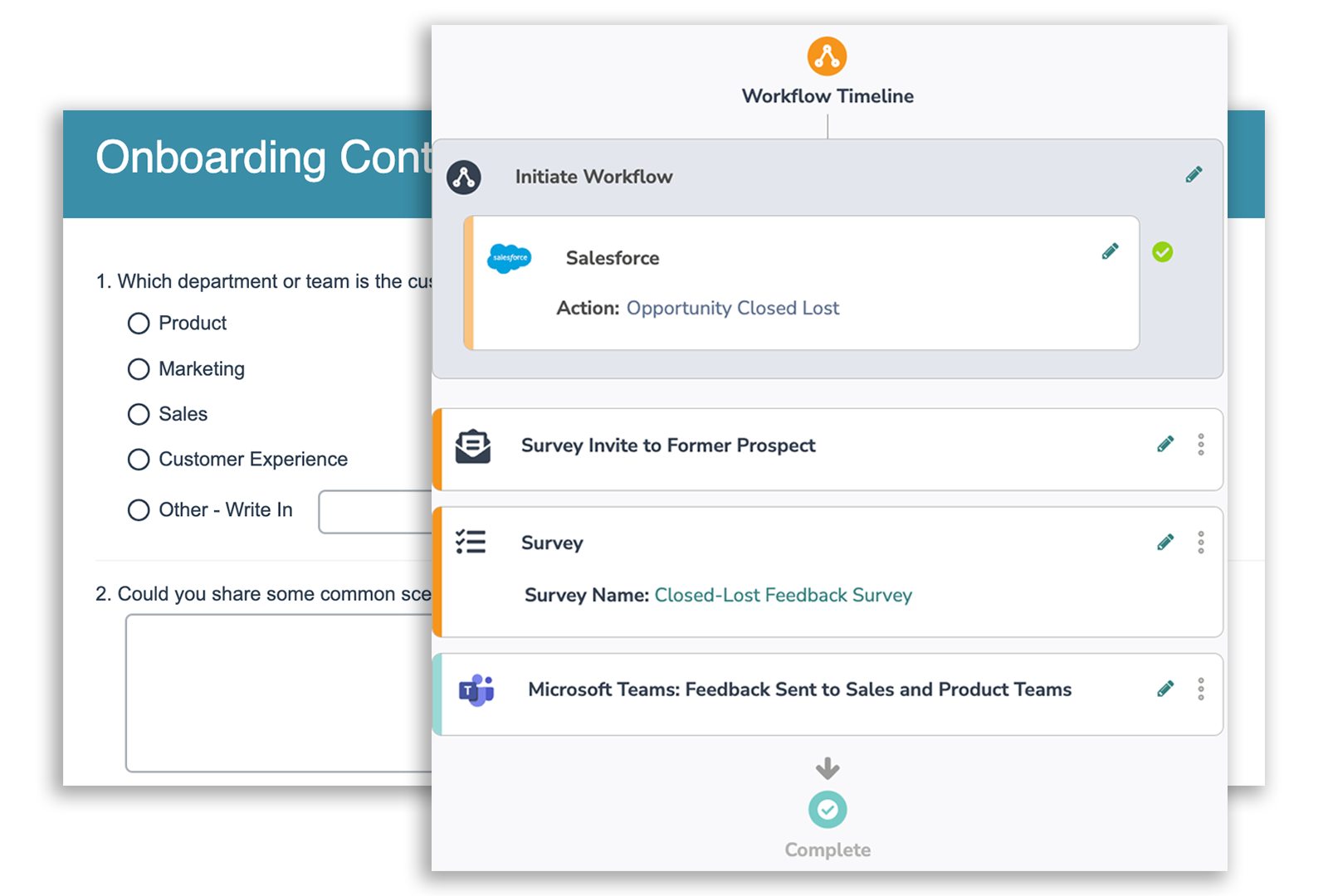
- Alchemer Workflow is the fastest, easiest, and most effective way to close the loop with customers.Learn More
- Alchemer Digital
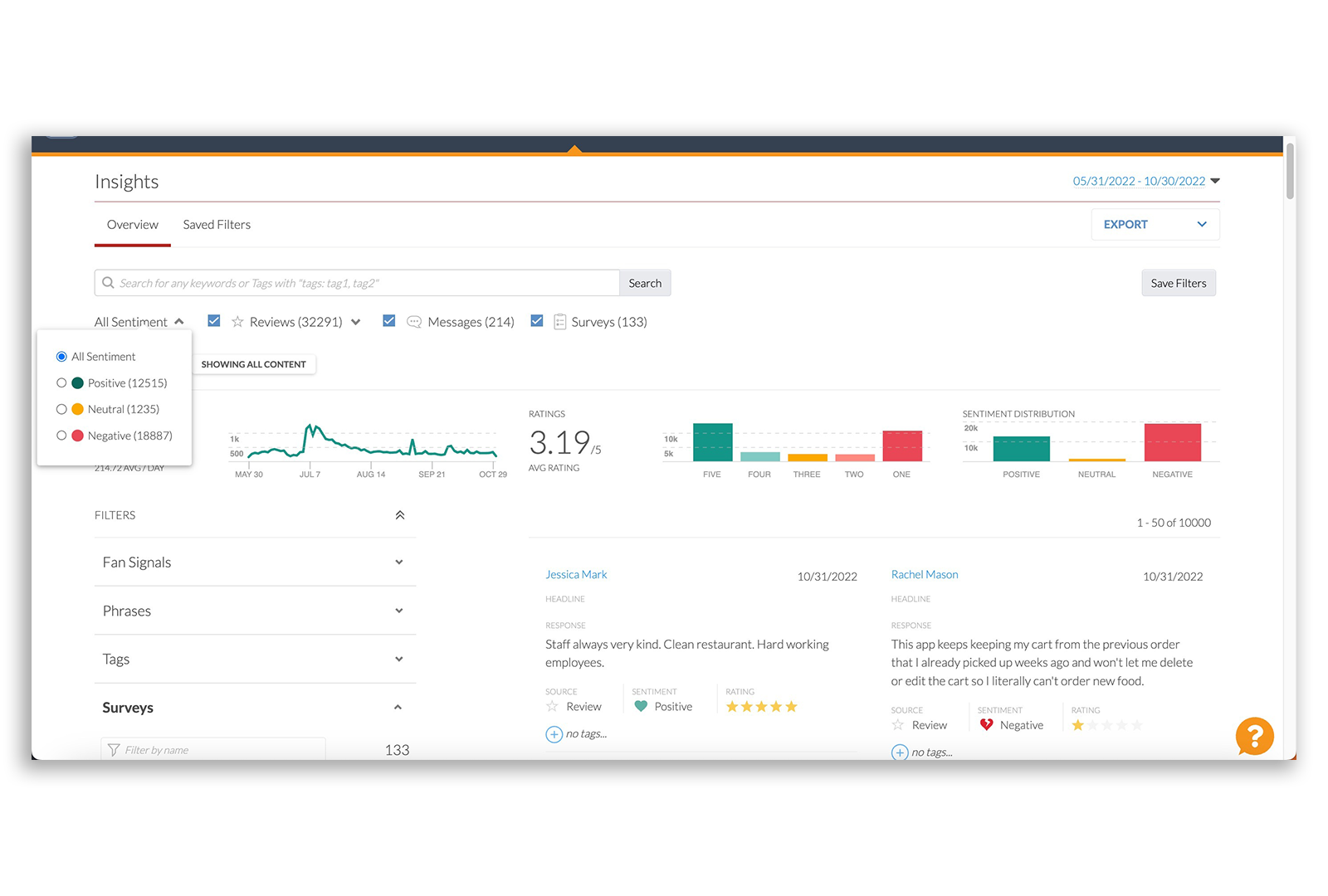
- Alchemer Digital drives omni-channel customer engagement across Mobile and Web digital properties.Learn More
-
- Services
- Panel Services
- Our full-service team will help you find the audience you need.Learn More
- Professional Services
- Specialists will custom-fit Alchemer Survey and Workflow to your business.Learn More
- Mobile Executive Reports
- Get help gaining insights into mobile customer feedback tailored to your requirements.Learn More
- Self-Service Survey Pricing
- Company